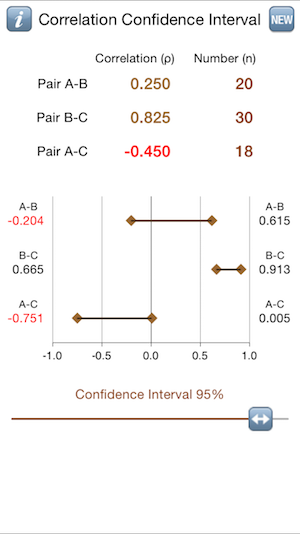
Correlation Confidence Intervals

Correlation is a quantitative tool commonly used by researchers to separate data sets into independent subgroups. Hypothesis testing determines whether or not the subgroups are numerically distinct. The degree to which the researcher can say the subgroups are distinct depends upon the overlap between the subgroups measured by the confidence interval estimates. The confidence interval estimates reflect the reality that there are errors in all quantitative estimates.

If correlation estimates were normally distributed, estimates of confidence intervals would be straightforward. However, correlation estimates are bound within the range of –1.0 to +1.0. The common technique devised by R.A. Fisher involves a nonlinear transformation of correlation functions into random variables that are approximately normal. The technique is known as Fisher's z-transformation and is formally expressed as ρ = tanh(z), where tanh( ) is the hyperbolic tangent function.

More simply, the transformed standard error, z, is defined as z = (1/2) ln[ (1 + ρ) / (1 – ρ) ]. The variance is a function of the number of paired samples in the sets being correlated and is defined as var(z) = 1 / (n – 8/3).

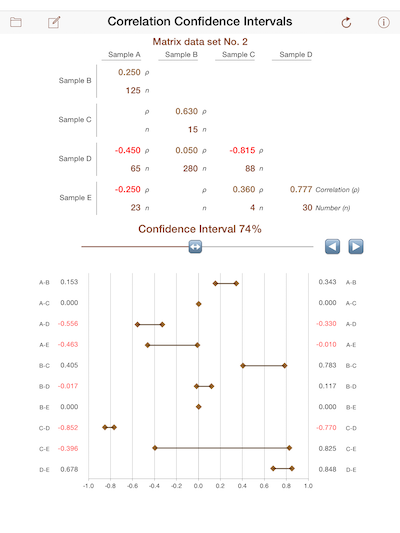
Thus, for example, the 95% confidence interval around a correlation estimate would be from (z – 1.96 σ) to (z + 1.96 σ) where σ = sqrt( 1/ (n – 8/3) ).

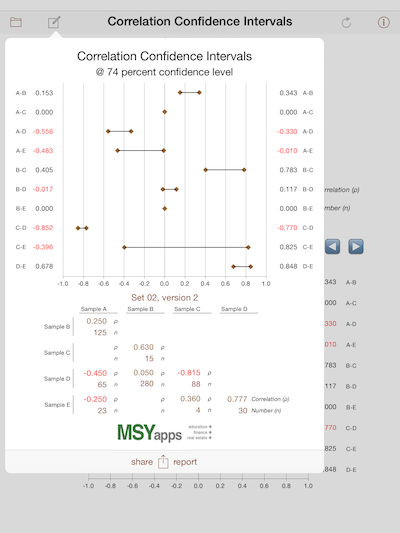
The iPad version allows you to add, retrieve, reorder, or delete data sets. Also, you may email, send via texting, and print data and results.

changes in version 7.3

• Updates to newer versions of iOS
• Various code changes

changes in version 7.1

• Bug fixes in iPhone version related to +/– correlation coefficient data entry and clearing of data
• Added Facebook and Twitter links
• Code improvements
• GUI changes
• Added continuous increase or decrease in confidence interval setting in iPad version

changes in version 4.0

• iPad version now adds email, text message, and print capability. A PDF report at a resolution of 72 dpi is available for sharing
• Streamlined and improved source code
• GUI improvements

changes in version 3.0

• Major rewrite and redesign for iOS 7
• Bug fixes

change in version 2.0

• Major revision that includes the option of adding data sets, retrieving saved sets, and deleting or reordering the saved sets